Normalised Mutual information replaces Correlation

The objective of this post is to introduce normalised Mutual Information as a better metric of co-dependency between two variables

Physical meaning: Correlation is a good measure of co-dependency as it is bounded between [0 to 1], and is simple to understand. However, it suffers from a drawback in that it only measures the linear relationship between two variables. If the relationship between two variables is non-linear, as is frequently the case in financial data, we will have low values of correlation, though the variables maybe perfectly predictable using a non-linear function. 

Normalised Mutual information is a standardised measure that overcomes these drawbacks. It is based on Information Theory, as opposed to correlation [Linear Algebra], and can accurately quantify the extent to which a relationship exists between two variables [Linear or Non-Linear]. We can then use ML techniques to model the relationship

Experimental results: Using Python code below

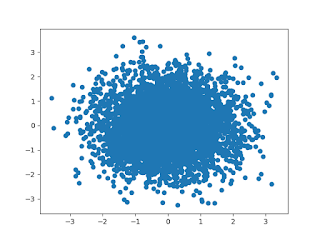
1. Zero Linear Relationship

Value of Correlation Coefficient obtained: 0.00023238753770240598

Value of normalised Mutual Information obtained: 0.005221150748814422

2. Perfect Linear Relationship:


Value of Correlation Coefficient obtained: 0.9999508615918137

Value of normalised Mutual Information obtained: 0.9476343636611047

In the code below, you will see that though the relationship appears normal, we have added a random noise component into the relationship. The Correlation coefficient does not seem to pick this up given the high correlation coefficient. However, the mutual information metric is more sensitive to this, and discounts accordingly.

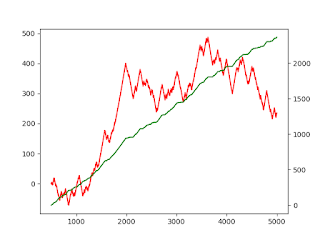
3. Non Linear Relationship:


Value of Correlation Coefficient obtained: 0.0159978574434585

Value of normalised Mutual Information obtained: 0.5406030932541388

The chart shows that the relationship is non-linear but predictable. The Correlation coefficient does not pick this up as the relationship is not linear, and says there is no relationship. If we use this metric as our guide, we will fail to pick up an opportunity for modeling a relationship. The mutual information recognises a form of relationship and accordingly assigns a higher value of 0.5. This is understandable, as an examination of the chart, will reveal that there are only two possible values of x for every value of y. 

Python code:

File: Normalised-Mutual-Information.py
# Import Libraries
import numpy as np
import scipy.stats as ss
from sklearn.metrics import mutual_info_score
import matplotlib.pyplot as plt

# Generate data
seed, samples = 0, 5000
x = np.random.normal(size = samples)
e = np.random.normal(size=samples)

# Define the relationship
y = (100 * np.abs(x)) + e

# Calculate the Correlation Coefficient
corr = np.corrcoef(x,y) [0,1]

# Calculate the normalised Mutual Information
hX = ss.entropy(np.histogram(x)[0])
hY = ss.entropy(np.histogram(y)[0])
cXY = np.histogram2d(x,y) [0]
iXY = mutual_info_score(None, None,contingency=cXY)
iXYn = iXY/min(hX,hY)

print(corr,iXYn)

# Plot the data
plt.scatter(x,y)
plt.show()

Comments

Post a Comment

Popular posts from this blog

1.2 Structured Data: Information Driven Bars

Image
This post will describe how to process & store High Frequency financial data to support your Machine Learning Algorithm, based on how much information is contained in the data The post is directly based on content from the book "Advances in Financial Machine Learning" from Marcos Lopez de Prado Physical meaning: This approach is inspired by Claude Shannon's Information Theory, that is the basis of most compression algorithms. Shannon argued that only departure from the norm is new information. A famous example, is that the sun has risen in the morning. Yes, the event has happened, but because the probability of this event was 1.0, this event does not represent information. In information driven bars, we attempt to use the same insight, to compress the financial data. Here, we know that financial data is inherently noisy, and put guardrails around what level of variance we expect for a particular behavior. It is only when the variance exceeds these guardrails, that we ...
Read more

2.1 Labeling: Fixed Horizon Method

Image
This post will describe how to assign labels to bars (financial features) to support supervised learning. Upon successful training, the algorithm will be able to predict the probability of a label once a bar (financial feature) has been observed. The post is directly based on content from the book "Advances in Financial Machine Learning" from Marcos Lopez de Prado Physical meaning: Algorithm description: Python code: import numpy as np import pandas as pd import matplotlib.pyplot as plt # Import data df = pd.read_csv( r'C:\Users\josde\OneDrive\Denny\Deep-learning\Data-sets\Trade-data\ES_Trades.csv' ) df = df.iloc[: , 0 : 5 ] df[ 'Dollar' ] = df[ 'Price' ]*df[ 'Volume' ] # Generate thresholds d = pd.DataFrame(pd.pivot_table(df , values = 'Dollar' , aggfunc = 'sum' , index = 'Date' )) DOLLAR_THRESHOLD = ( 1 / 50 )*np.average(d[ 'Dollar' ]) # Generate bars def bar_gen (df , DOLLAR_THRESHOLD): collector , dollarb...
Read more

2.2 Labeling: Triple barrier method

Image
 This post will describe how to label a financial dataset to support supervised learning The post is directly based on content from the book "Advances in Financial Machine Learning" from Marcos Lopez de Prado Physical meaning: Algorithm description: Python code: # Import libraries import numpy as np import pandas as pd import matplotlib.pyplot as plt import math # Import data df = pd.read_csv( r'C:\Users\josde\OneDrive\Denny\Deep-learning\Data-sets\Trade-data\ES_Trades.csv' ) df = df.iloc[: , 0 : 5 ] df[ 'Dollar' ] = df[ 'Price' ] * df[ 'Volume' ] print (df.columns) # Generate thresholds d = pd.DataFrame(pd.pivot_table(df , values = 'Dollar' , aggfunc = 'sum' , index = 'Date' )) DOLLAR_THRESHOLD = ( 1 / 50 ) * np.average(d[ 'Dollar' ]) # Generate bars def bar_gen (df , DOLLAR_THRESHOLD): collector , dollarbar_tmp = [] , [] dollar_cusum = 0 for i , (price , dollar) in enumerate ( zip (df[ 'Price...
Read more